La méthode de Cardan pour résoudre des équations insolubles

Les nombres complexes sont une extension des nombres réels et se présentent sous la forme a+bi+bi, où a et bbsont des nombres réels, et ii est l'unité imaginaire satisfaisant i2=−1. Cette extension est particulièrement utile pour résoudre des équations qui ne possèdent pas de solution dans l'ensemble des nombres réels.

La formule de Cardan est un exemple remarquable d'application des nombres complexes dans la résolution d'équations cubiques, c'est-à-dire des équations de la forme ax3+bx2+cx+d=0. Établie au XVIe siècle par le mathématicien italien Gerolamo Cardano, cette formule offre une méthode pour trouver les racines d'une telle équation.

Pour simplifier, considérons une équation cubique réduite de la forme $x^3+px+q=0$. La formule de Cardan s'exprime alors comme suit :

​

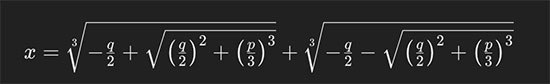
Dans cette expression, le terme sous la racine carrée,  peut être négatif, ce qui mène à des racines carrées de nombres négatifs et donc à l'utilisation de nombres complexes. C'est précisément dans de tels cas que les nombres complexes deviennent indispensables pour exprimer les solutions de l'équation.

Les solutions obtenues peuvent être réelles ou complexes, selon les valeurs de p et q. Cette formule démontre la puissance des nombres complexes en mathématiques, permettant de résoudre des équations qui, autrement, ne pourraient pas l'être dans le cadre des nombres réels seuls. La formule de Cardan illustre ainsi comment l'introduction des nombres complexes a significativement élargi le champ des possibles en algèbre.

---------------

Gerolamo Cardano, né en 1501 à Pavie et décédé en 1576, fut un mathématicien, médecin, astronome et philosophe italien de la Renaissance. Figure éminente de son époque, le scientifique est surtout connu pour ses contributions significatives dans les domaines des mathématiques et de la science. Parmi ses réalisations les plus célèbres figure la publication de la formule de résolution des équations cubiques, communément appelée la formule de Cardan. Cette découverte a marqué un tournant dans l'histoire des mathématiques, car elle a fourni une méthode systématique pour résoudre une classe entière d'équations auparavant considérées comme insolubles. Outre ses travaux en algèbre, Cardano a également écrit sur la probabilité, faisant de lui l'un des pionniers dans l'étude de cette discipline. Sa curiosité insatiable l'a également amené à explorer divers autres champs, y compris la mécanique et l'astrologie, bien que cette dernière ait suscité controverses et critiques. Malgré les défis personnels et professionnels auxquels il a été confronté tout au long de sa vie, l'héritage du mathématicien en tant que polymathe de la Renaissance reste profondément ancré dans l'histoire de la science.
----------------

A voir : INTRODUCTION AUX NOMBRES COMPLEXES. FORMULE DE CARDAN

Lire :