
Conjecture de Brumer-Stark en mathématiques
La conjecture de Brumer-Stark est une conjecture en théorie des nombres algébriques qui concerne les valeurs spéciales de certaines fonctions L associées à des courbes elliptiques sur des corps de nombres.
Plus précisément, la conjecture affirme que la partie algébrique du terme principal du développement en série de Taylor de la fonction L en un certain point critique peut être exprimée en termes de certains invariants arithmétiques de la courbe elliptique, notamment son conducteur et l'ordre de son groupe de Tate-Shafarevich.
La conjecture a été proposée indépendamment par B. Brumer et H. M. Stark dans les années 1970, et elle a depuis fait l'objet de nombreuses recherches en théorie des nombres. Bien que certains résultats partiels aient été obtenus, la conjecture reste ouverte dans sa pleine généralité.
---------------
La série de Taylor est un outil mathématique efficace qui permet d'approximer des fonctions à l'aide de polynômes. Cette série repose sur le développement d'une fonction autour d'un point spécifique, généralement noté \(a\), et elle s'exprime comme la somme des dérivées de la fonction en ce point, multipliées par une puissance de la différence entre la variable de la fonction et le point \(a\), le tout divisé par le factoriel de l'ordre de la dérivée. Formellement, la série de Taylor d'une fonction \(f\) autour du point \(a\) est donnée par :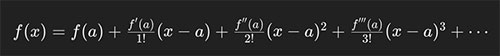
où \(f^{(n)}(a)\) représente la \(n\)-ième dérivée de \(f\) évaluée en \(a\), et \(n!\) est le factoriel de \(n\). Cette expression permet d'obtenir une approximation de \(f(x)\) par un polynôme de degré fini lorsque l'on considère un nombre fini de termes de la série, offrant ainsi un outil précieux pour l'analyse et l'approximation de fonctions dans divers domaines des mathématiques et de la physique. La série de Taylor joue un rôle crucial en analyse numérique, en théorie des probabilités, et dans le cadre de la résolution de nombreuses équations différentielles et problèmes d'ingénierie.
--------------
Lire :