
L'analyse harmonique pour étudier les fonctions périodiques
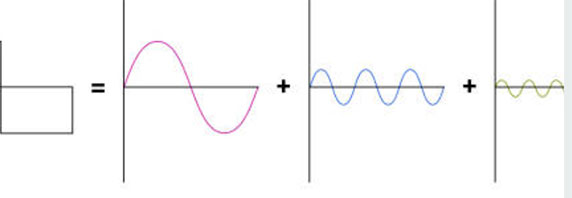
L'analyse harmonique est une méthode utilisée en mathématiques, en physique et dans bien d'autres domaines pour étudier les fonctions périodiques ou presque périodiques, comme les signaux électriques, les ondes sonores, les mouvements planétaires, etc. Elle repose sur le principe que toute fonction périodique peut être représentée comme une somme (ou une intégrale) de fonctions sinus et cosinus, appelées harmoniques.
Le processus d'analyse harmonique implique généralement plusieurs étapes :
1. **Décomposition de la fonction périodique en série de Fourier :** La série de Fourier est une expression mathématique qui représente une fonction périodique comme une somme infinie de fonctions sinus et cosinus, chacune avec une amplitude et une fréquence spécifiques. Cette décomposition permet de transformer la fonction périodique complexe en une série de composantes plus simples.
---------
La série de Fourier est une méthode mathématique fondamentale utilisée pour représenter une fonction périodique comme une somme infinie (ou une intégrale) de fonctions sinus et cosinus. Elle porte le nom du mathématicien français Joseph Fourier, qui a développé cette technique au début du 19e siècle. La série de Fourier est largement utilisée dans de nombreux domaines, notamment en mathématiques, en physique, en ingénierie, en traitement du signal, en télécommunications, en acoustique, et dans d'autres domaines où des phénomènes périodiques sont observés.
Formellement, la série de Fourier d'une fonction périodique \( f(x) \) de période \( T \) est donnée par :
où a00, ann, et bnn
sont les coefficients de Fourier, qui peuvent être calculés à l'aide d'intégrales définies ou de méthodes algébriques. Ces coefficients déterminent l'amplitude et la phase des composantes sinus et cosinus de la série de Fourier.
La série de Fourier permet de décomposer une fonction périodique complexe en une somme pondérée de composantes sinus et cosinus, appelées harmoniques. Cette représentation permet de simplifier l'analyse et la manipulation de la fonction périodique, ainsi que de comprendre sa structure et son comportement dans le domaine fréquentiel.
La convergence de la série de Fourier dépend des propriétés de la fonction périodique étudiée. Pour certaines fonctions, la série de Fourier converge uniformément et représente exactement la fonction périodique. Pour d'autres fonctions plus complexes, la série de Fourier peut converger seulement dans un sens ponctuel ou en moyenne quadratique, nécessitant parfois des approximations pour obtenir une représentation précise.
-----------
2. **Calcul des coefficients de Fourier :** Les coefficients de Fourier sont des valeurs numériques qui déterminent l'amplitude et la phase de chaque composante sinus ou cosinus dans la série de Fourier. Ils sont calculés en effectuant des intégrations ou des calculs algébriques sur la fonction périodique d'origine.
3. **Interprétation des résultats :** Une fois les coefficients de Fourier calculés, ils peuvent être utilisés pour analyser différents aspects de la fonction périodique, tels que son spectre de fréquences, son amplitude relative à chaque composante harmonique, sa phase, etc. Cette analyse permet de comprendre la structure et le comportement de la fonction périodique, ainsi que de prédire son évolution dans le temps.
L'analyse harmonique est largement utilisée dans de nombreux domaines, notamment en ingénierie, en physique, en musique, en économie et en géologie, pour analyser et interpréter les signaux périodiques et les phénomènes périodiques observés dans la nature et dans les systèmes artificiels. Elle constitue un outil puissant pour la modélisation, la prédiction et la résolution de nombreux problèmes pratiques.