La composition des vitesses : un principe fondamental de la relativité restreinte

Cette question touche à un principe fondamental de la relativité restreinte, formulée par Albert Einstein. En effet, selon les lois de la physique classique, notamment celles de Galilée, si un objet A se déplace à une certaine vitesse v par rapport à un objet B, et cet objet B se déplace à une certaine vitesse u par rapport à un objet C, alors la vitesse de A par rapport à C est simplement la somme des vitesses v+u.

Cependant, cette addition simple des vitesses ne tient pas dans le contexte de vitesses approchant celle de la lumière. Einstein a montré que pour des vitesses relativistes, c'est-à-dire proches de la vitesse de la lumière, il faut utiliser une formule plus complexe pour calculer la vitesse relative. Cette formule est issue de la théorie de la relativité restreinte et assure que la vitesse de la lumière reste constante et maximale dans tous les référentiels, un postulat clé de la relativité.

La formule pour l'addition des vitesses en relativité restreinte est la suivante :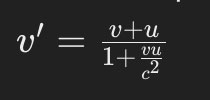

où :
- v' est la vitesse de A par rapport à C,
- v est la vitesse de A par rapport à B,
- u est la vitesse de B par rapport à C,
- c est la vitesse de la lumière dans le vide.

Cette formule garantit que même si v et u sont très grandes, la vitesse résultante v' ne dépasse jamais c, la vitesse de la lumière. Cela illustre une différence fondamentale entre la physique newtonienne et la physique relativiste, soulignant l'incapacité d'atteindre ou de dépasser la vitesse de la lumière pour des objets ayant une masse.