
Mécanique quantique : la forme temporelle et la forme indépendante du temps
L'équation de Schrödinger est une équation fondamentale en mécanique quantique qui décrit comment l'état quantique d'un système physique évolue dans le temps. Elle a été formulée par Erwin Schrödinger en 192, centrale pour la compréhension des systèmes quantiques. L'équation existe sous deux formes principales : la forme dépendante du temps et la forme indépendante du temps, chacune ayant ses propres applications et implications.
Forme Temporelle (Dépendante du Temps
La forme temporelle de l'équation de Schrödinger prend en compte l'évolution temporelle des états quantiques. Elle est exprimée par la relation suivante :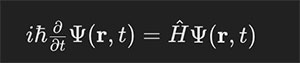
où \(i\) est l'unité imaginaire, \(\hbar\) est la constante de Planck réduite, \(\Psi(\mathbf{r}, t)\) est la fonction d'onde du système, qui dépend de la position \(\mathbf{r}\) et du temps \(t\), et \(\hat{H}\) est l'opérateur hamiltonien du système, qui représente l'énergie totale (cinétique plus potentielle). Cette équation montre comment la fonction d'onde, qui contient toute l'information possible sur le système, évolue avec le temps.
Forme Indépendante du Temps
La forme indépendante du temps de l'équation de Schrödinger est utilisée pour des systèmes où l'énergie totale est conservée, c'est-à-dire dans des situations stationnaires où l'opérateur hamiltonien ne dépend pas explicitement du temps. Cette forme de l'équation est écrite comme suit :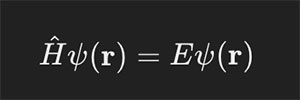
Ici, \(\psi(\mathbf{r})\) est une fonction d'onde qui ne dépend que de la position, et \(E\) représente les niveaux d'énergie possibles du système. Cette équation permet de calculer les états énergétiques stationnaires (ou états propres) et leurs énergies associées pour un système quantique. Elle joue un rôle crucial dans la détermination des structures électroniques des atomes et des molécules, ainsi que dans la compréhension des liaisons chimiques.
L'introduction de l'équation de Schrödinger a marqué un tournant dans la physique, permettant une compréhension et une prédiction précises des phénomènes quantiques. Elle a posé les bases pour le développement de la chimie quantique, la physique des solides, et a profondément influencé de nombreux autres domaines de la science. La distinction entre les formes temporelle et indépendante du temps de l'équation permet aux physiciens et chimistes de choisir l'approche la plus adaptée à l'étude de différents systèmes et processus quantiques.